Research Projects

Stability Analysis in two-phase cartesian coordinates

Stability analysis tool developed for a 2D liquid planar sheet injected into gas. Perturbation equations are obtained by applying symmetric (varicose) and asymmetric (sinuous) perturbations over the mean flow. The perturbation equations are solved using Chebyshev spectral method to determine whether the applied perturbation is stable or unstable.

Schematic of symmetric (varicose) disturbance:

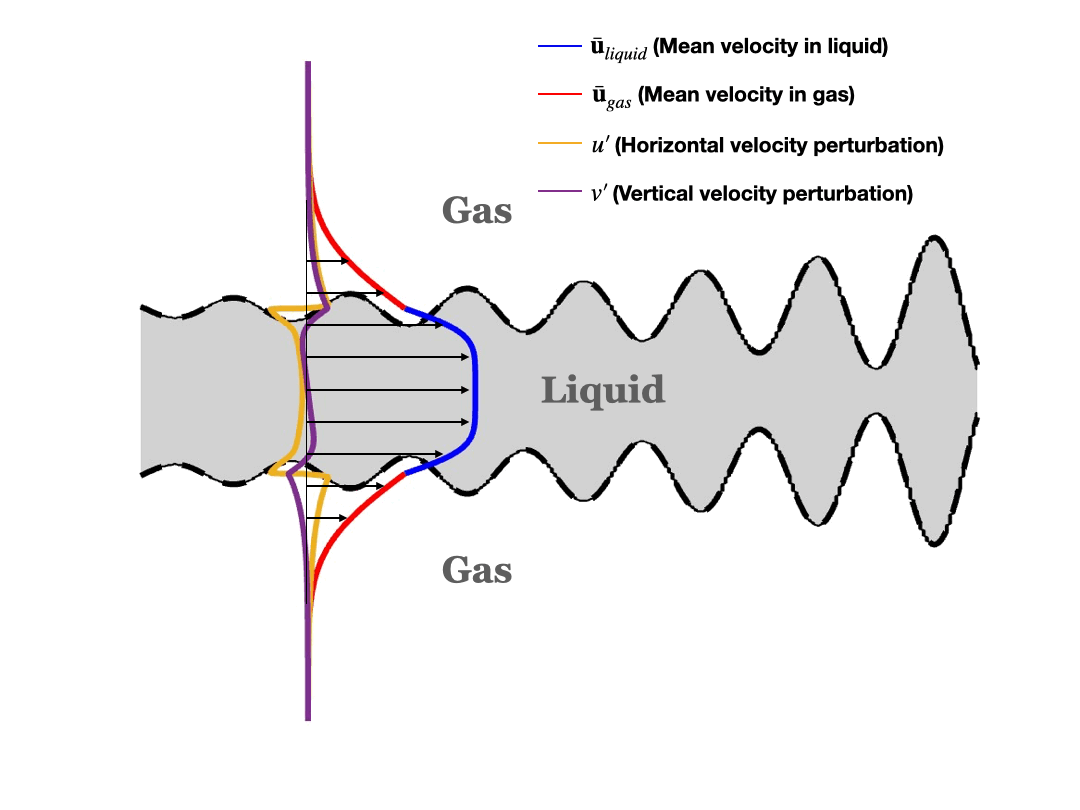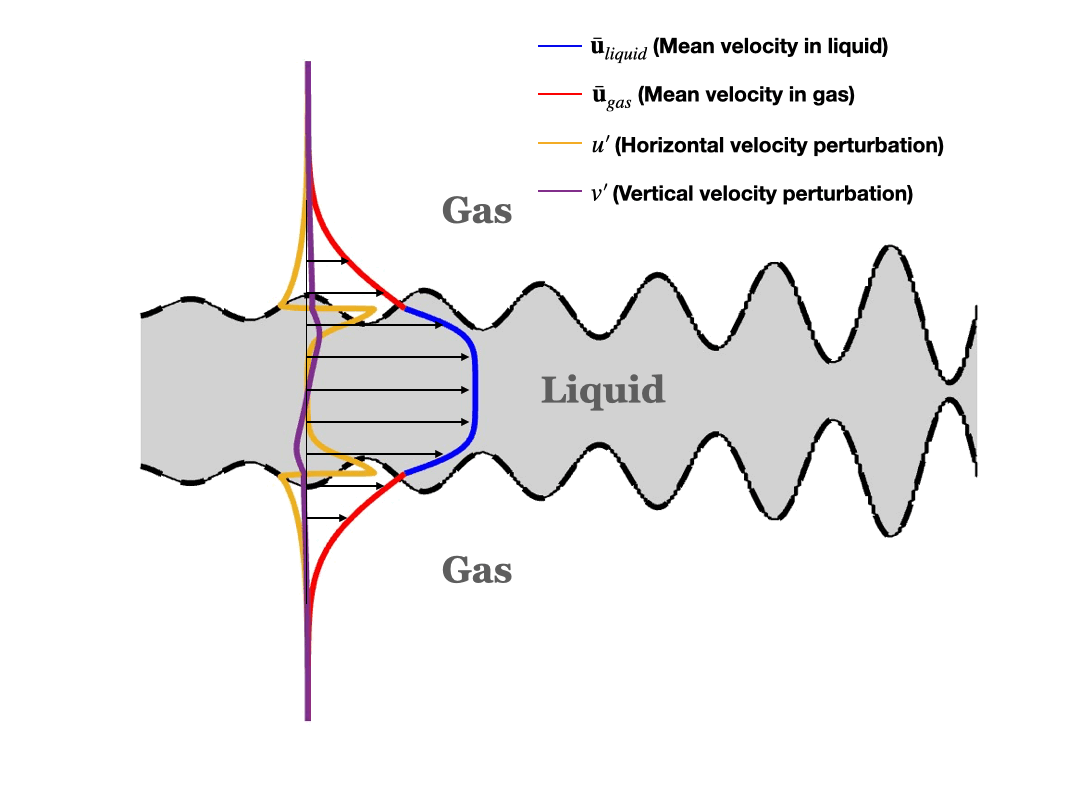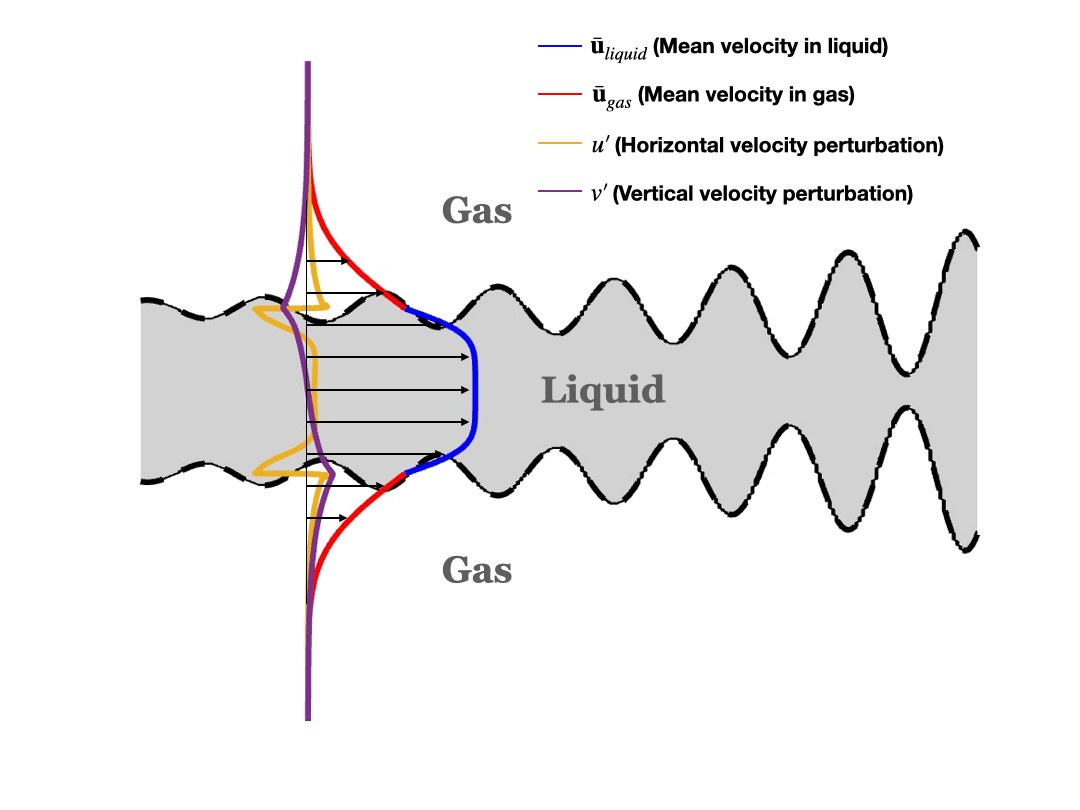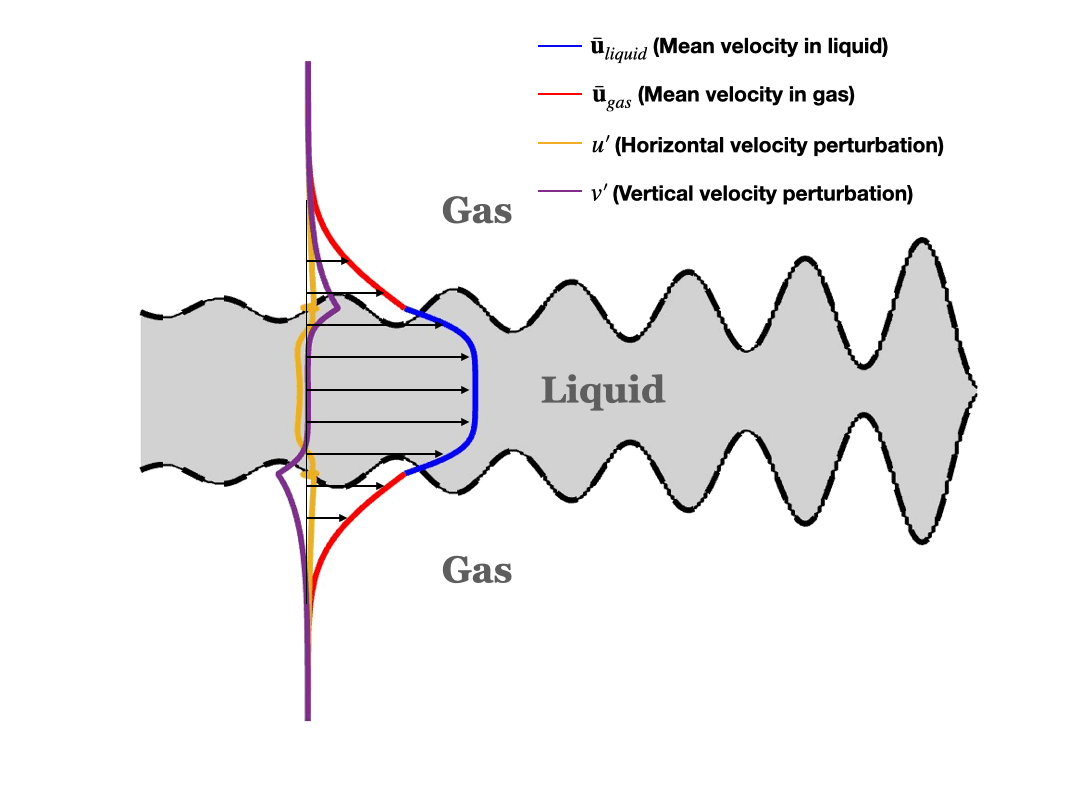
Schematic of asymmetric (sinuous) disturbance:

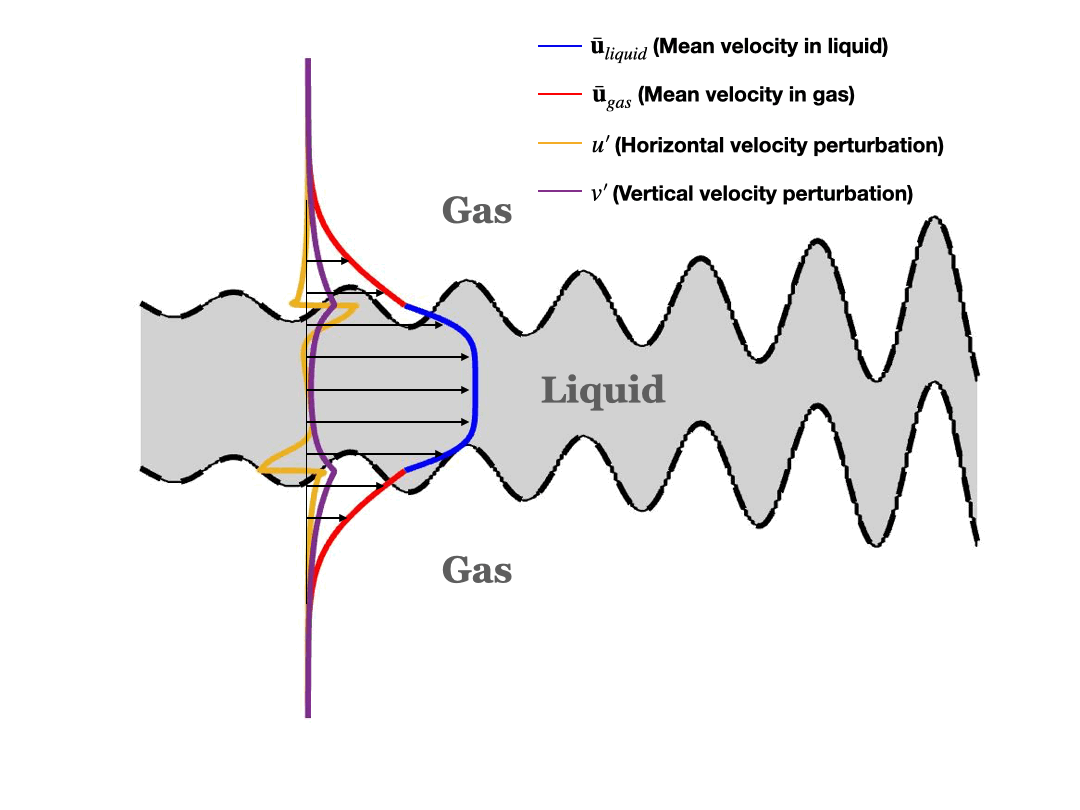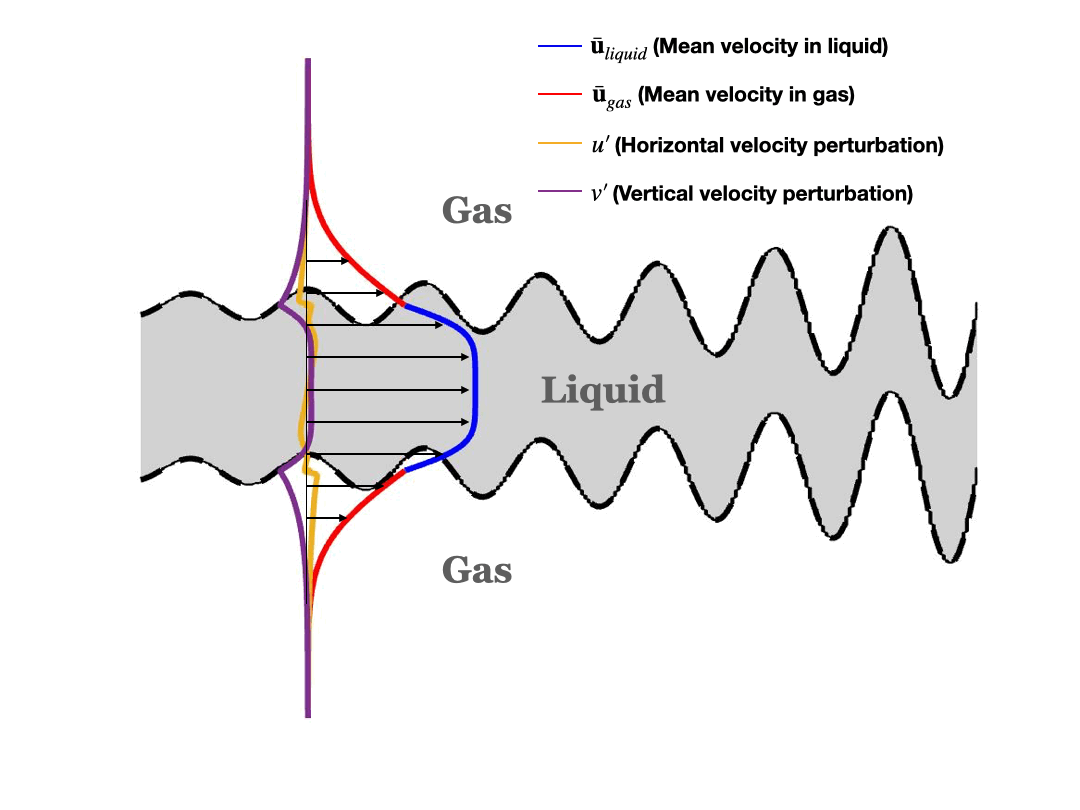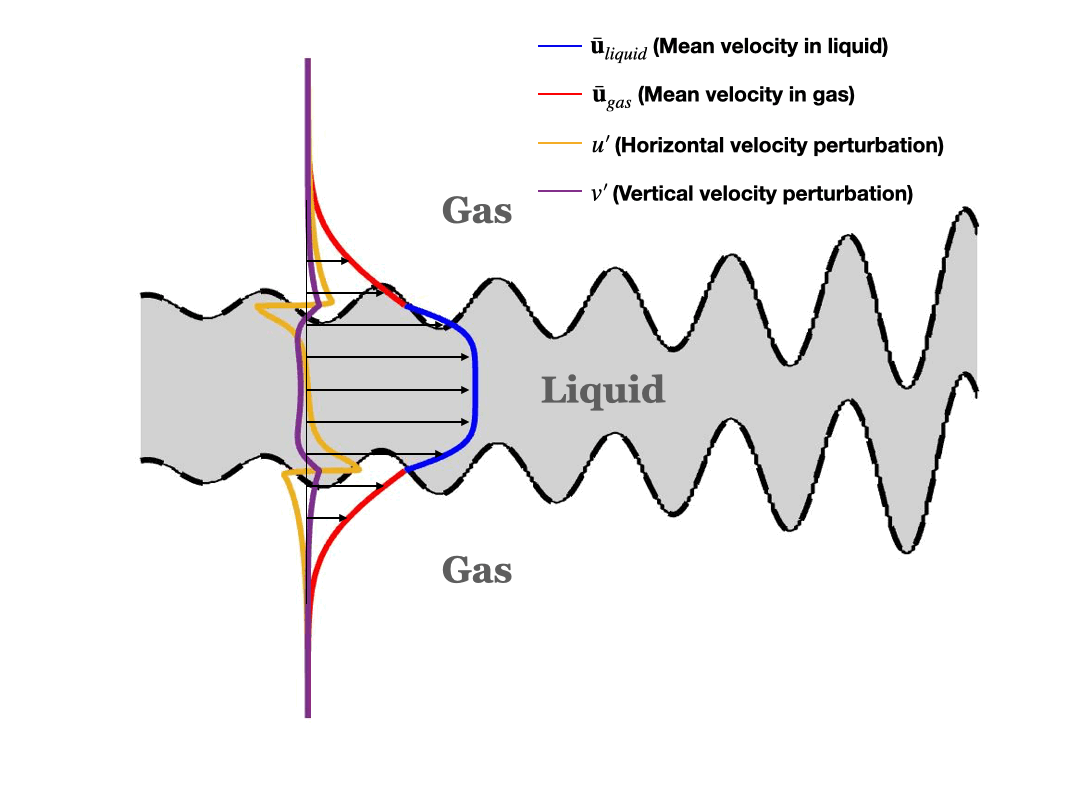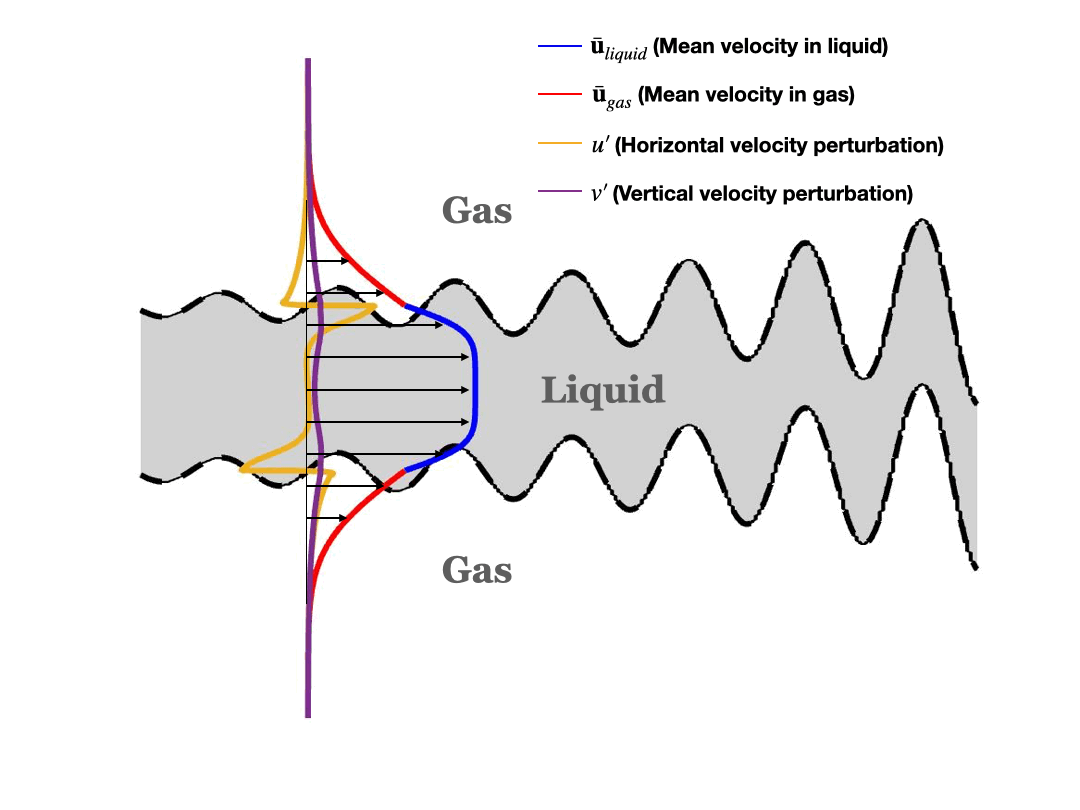
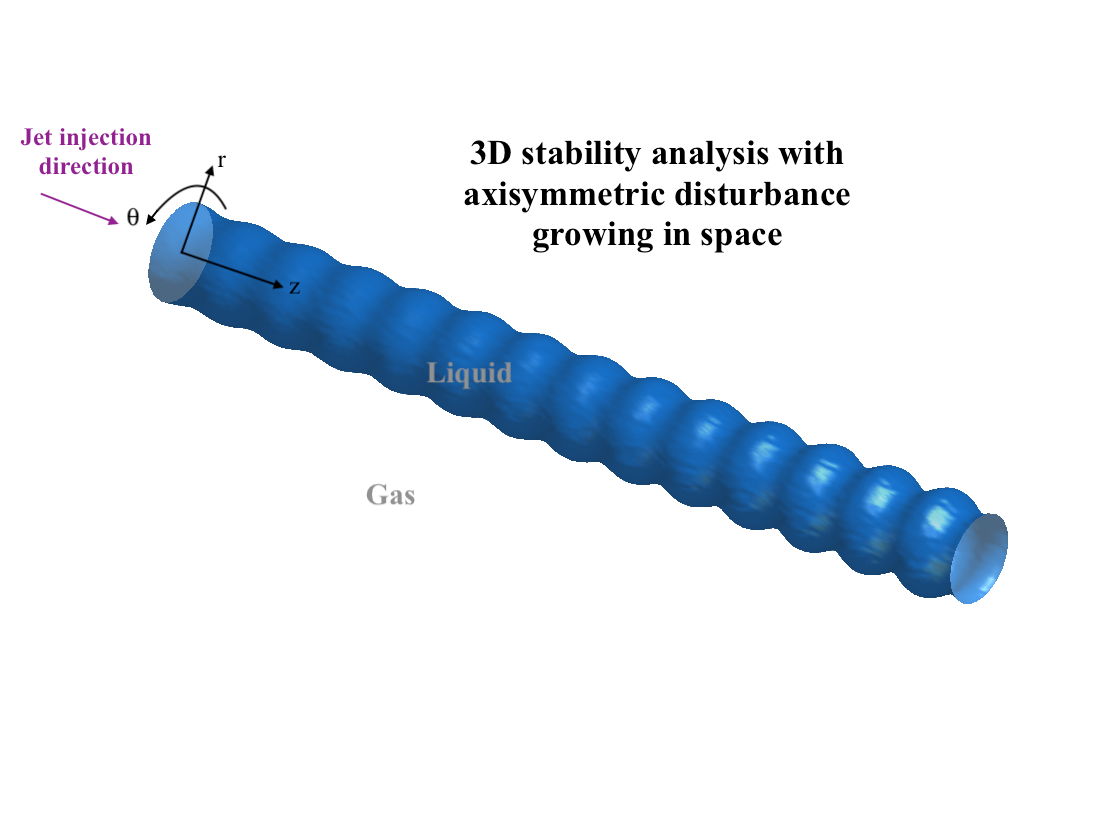
Stability Analysis in two-phase cylindrical coordinates

Stability analysis tool developed for a 3D cylindrical liquid jet injected into gas. Perturbation equations are obtained by applying axisymmetric and asymmetric (helical) perturbations over the mean flow. The perturbation equations are solved using Chebyshev spectral method to determine whether the applied perturbation is stable or unstable.

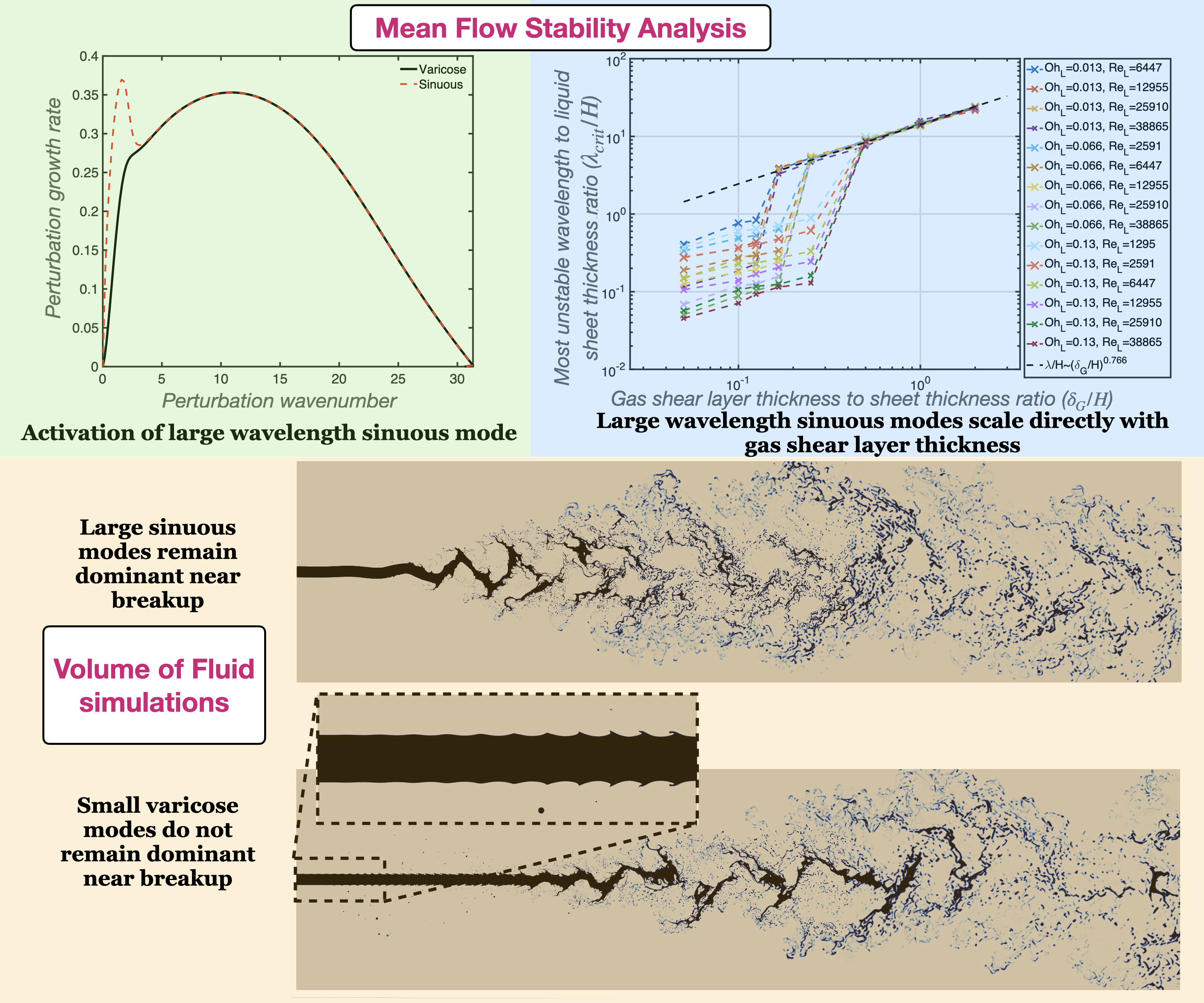
Large-scale modes observed in liquid sheet breakup

The breakup of liquid sheets is caused by large wavelength sinuous modes which are activated at high gas shear layer thickness. The animation below shows a high-speed liquid sheet injected into air. There are disturbances created on the surface, and the liquid core breaks up due to large wavelength asymmetric (sinuous) mode disturbances.

The underlying physics of these sinuous modes are explained using Spatial mean flow stability analysis and high-fidelity Volume of Fluid simulations. An overview of the project is given using the figure below: